熱中症搬送人員数に日最高気温と平均水蒸気圧が強く影響することは疑いの余地がない.他の気象条件として風速や雲量が負の影響をおよぼす可能性はないだろうか.言い換えると,風速が強ければ熱中症を発症する可能性が下がることは考えられないか,晴れよりも曇りや雨の日は熱中症を発症する可能性が下がることは考えられないかということである.
前回の記事で熱中症データベースに平均風速をインポートした.詳細は割愛するが,同様の手順で平均雲量のデータもインポートできる.
今回は説明変数として日最高気温,平均水蒸気圧に平均風速および平均雲量を加えて一般化線形モデルにて解析を行い,tree関数で可視化を試みた.
SQL Serverからデータを抽出
クエリ
下記クエリを発行して結果をEXCELにコピペして保存する.ファイル名をHeatStroke3.xlsxとする.
USE HeatStrokeDB; GO SELECT P.FiscalYear , T.年月日 AS Date , T.都道府県コード AS PrefCode , T.都道府県 AS Pref , T.日最高気温 AS Temp , V.日平均蒸気圧 AS Vapor , W.平均風速 AS Wind , C.平均雲量 AS Cloud , P.Population AS Pop , H.[搬送人員(計)] AS Num FROM dbo.T_HeatStroke AS H INNER JOIN dbo.T_MaxTemperature AS T ON H.都道府県コード = T.都道府県コード AND H.日付 = T.年月日 INNER JOIN dbo.T_VaporPressure AS V ON H.都道府県コード = V.都道府県コード AND H.日付 = V.年月日 INNER JOIN dbo.T_Wind AS W ON H.都道府県コード = W.都道府県コード AND H.日付 = W.年月日 INNER JOIN dbo.T_Population AS P ON H.都道府県コード = P.PrefCode AND YEAR(H.日付) = P.FiscalYear INNER JOIN dbo.T_Cloud AS C ON H.都道府県コード = C.都道府県コード AND H.日付 = C.年月日 ORDER BY PrefCode, Date
(63725 行処理されました)
Rでの処理
データの読み込み
ユーザーインターフェースでHeatStroke3.xlsxを読み込む.
> library(readxl)
> HeatStroke3 <- read_excel("C:/Users/***/HeatStroke3.xlsx",
+ col_types = c("numeric", "date", "numeric",
+ "text", "numeric", "numeric", "numeric",
+ "numeric", "numeric", "numeric"))
交互作用項を考慮した一般化線形回帰
下記コードを実行して変数y, x1, x2, x3, x4にそれぞれ熱中症搬送人員数,日最高気温,平均水蒸気圧,平均風速および平均雲量を代入する.
> y = HeatStroke3$Num > x1 = HeatStroke3$Temp > x2 = HeatStroke3$Vapor > x3 = HeatStroke3$Wind > x4 = HeatStroke3$Cloud
下記コードを実行してポアソン分布による一般化線形回帰分析を行う.アスタリスクは変数間の交互作用を示し,I()で囲んだ内容はべき乗を示している.これは変数の交互作用項を最大限取り入れた最大モデルである.
> w = glm(y ~ x1*x2*x3*x4 + I(x1^3) + I(x2^3) + I(x3^3) + I(x4^3) + I(x1^2) + I(x2^2) + I(x3^2) + I(x4^2), family = poisson(link = "log")) > summary(w)
下記が要約の結果である.
Call:
glm(formula = y ~ x1 * x2 * x3 * x4 + I(x1^3) + I(x2^3) + I(x3^3) +
I(x4^3) + I(x1^2) + I(x2^2) + I(x3^2) + I(x4^2), family = poisson(link = "log"))
Deviance Residuals:
Min 1Q Median 3Q Max
-10.2530 -1.8464 -0.8799 0.5294 31.1361
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.210e+00 8.736e-01 -3.674 0.000239 ***
x1 4.616e-01 6.442e-02 7.166 7.74e-13 ***
x2 -5.519e-01 2.738e-02 -20.159 < 2e-16 ***
x3 -1.305e+00 1.921e-01 -6.794 1.09e-11 ***
x4 -3.599e-01 7.864e-02 -4.576 4.74e-06 ***
I(x1^3) 1.297e-04 2.085e-05 6.224 4.85e-10 ***
I(x2^3) -1.578e-04 8.156e-06 -19.352 < 2e-16 ***
I(x3^3) 3.671e-03 5.739e-05 63.970 < 2e-16 ***
I(x4^3) -1.013e-03 7.300e-05 -13.877 < 2e-16 ***
I(x1^2) -1.279e-02 1.952e-03 -6.551 5.71e-11 ***
I(x2^2) 1.363e-02 5.742e-04 23.744 < 2e-16 ***
I(x3^2) -9.989e-02 1.439e-03 -69.428 < 2e-16 ***
I(x4^2) 1.692e-02 1.204e-03 14.054 < 2e-16 ***
x1:x2 8.065e-03 8.006e-04 10.073 < 2e-16 ***
x1:x3 5.922e-02 6.295e-03 9.407 < 2e-16 ***
x2:x3 8.176e-02 8.093e-03 10.104 < 2e-16 ***
x1:x4 8.070e-03 2.598e-03 3.106 0.001894 **
x2:x4 7.384e-03 3.231e-03 2.285 0.022301 *
x3:x4 2.217e-01 2.546e-02 8.707 < 2e-16 ***
x1:x2:x3 -2.493e-03 2.583e-04 -9.651 < 2e-16 ***
x1:x2:x4 -2.007e-04 1.042e-04 -1.926 0.054049 .
x1:x3:x4 -6.516e-03 8.489e-04 -7.676 1.64e-14 ***
x2:x3:x4 -9.417e-03 1.053e-03 -8.945 < 2e-16 ***
x1:x2:x3:x4 2.621e-04 3.426e-05 7.649 2.03e-14 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 1081688 on 63724 degrees of freedom
Residual deviance: 470950 on 63701 degrees of freedom
AIC: 635242
Number of Fisher Scoring iterations: 16
解釈
上記結果は解釈が難しい.交互作用項ほとんどすべてが有意となっている.しかし一つ一つ見ていくと,おかしいと思われる回帰係数が存在することがわかる.まず注目すべきは符号である.
符号が正の場合はその変数が増加すると,搬送人員数を増加させる方向に作用する.逆に符号が負の場合はその変数が増加すると,搬送人員数を減少させる方向に作用する.1次の項を見てみると,最高気温以外の変数が増加すると搬送人員数を減少させる方向に作用することになる.つまり平均水蒸気圧が増加すると搬送人員数が減少することになる.これは常識から考えておかしい.平均風速と平均雲量についてはとりあえず判断を保留する.
2次の項および3次の項については組み合わせによって符号が変わり,安定しない.
次に注目するのは推定値の大きさである.2次,3次の項は10のマイナス2乗からマイナス3乗,つまりゼロに近い.指数関数のゼロ乗はほとんど1であることを意味する.サンプルサイズが6.3万と極めて大きく,臨床的に意味のない統計的有意性が出てしまった可能性がある.
step関数で変数を減少させられるか
step関数で変数減少を試みる.
> w1 = step(w)
しかし,結果は以下のようであり,すべての変数が保存されている.summary関数で要約しても変数に変化はない.
Start: AIC=635242.4
y ~ x1 * x2 * x3 * x4 + I(x1^3) + I(x2^3) + I(x3^3) + I(x4^3) +
I(x1^2) + I(x2^2) + I(x3^2) + I(x4^2)
Df Deviance AIC
470950 635242
- I(x1^3) 1 470990 635280
- I(x1^2) 1 470994 635285
- x1:x2:x3:x4 1 471009 635299
- I(x4^3) 1 471142 635432
- I(x4^2) 1 471146 635437
- I(x2^3) 1 471316 635606
- I(x2^2) 1 471491 635782
- I(x3^3) 1 472259 636549
- I(x3^2) 1 473801 638091
最小モデルではどうか
一方,1次のみの最小モデルではどうなるか.すべての説明変数が有意であり,平均風速と平均雲量は搬送人員数に負の影響を及ぼしている.しかしAICだけで比較すると最小モデルの予測性能は最大モデルよりも低くなる.
> z = glm(y ~ x1 + x2 + x3 + x4, family = poisson(link = "log"))
> summary(z)
Call:
glm(formula = y ~ x1 + x2 + x3 + x4, family = poisson(link = "log"))
Deviance Residuals:
Min 1Q Median 3Q Max
-9.937 -1.902 -0.864 0.571 32.190
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -7.5387653 0.0197868 -381.00 <2e-16 ***
x1 0.2627224 0.0005947 441.79 <2e-16 ***
x2 0.0662424 0.0004304 153.92 <2e-16 ***
x3 -0.0276705 0.0012951 -21.36 <2e-16 ***
x4 -0.0372499 0.0005563 -66.96 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 1081688 on 63724 degrees of freedom
Residual deviance: 486213 on 63720 degrees of freedom
AIC: 650468
Number of Fisher Scoring iterations: 5
tree関数による可視化
視点を変えてみる.樹木モデルを当てはめて説明変数間に複雑な交互作用がないか調べてみる.
> library(tree) > z = tree(y ~ x1 + x2 + x3 + x4) > plot(z) > text(z)
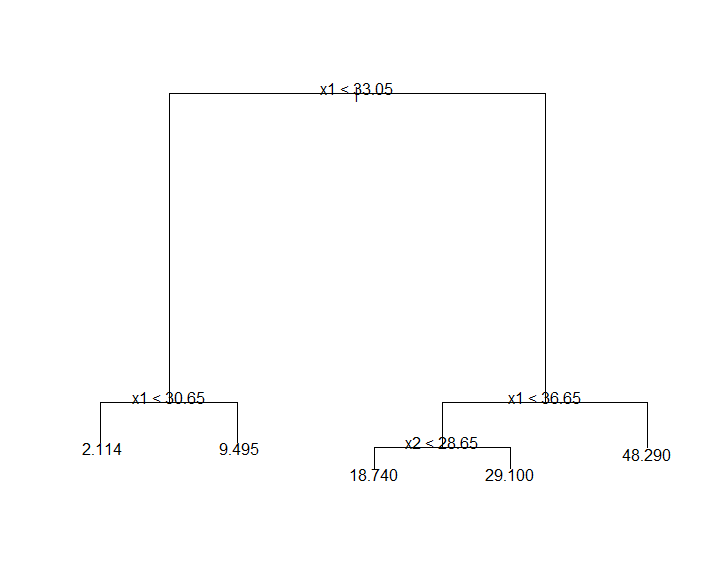
x1とx2以外の説明変数は搬送人員数に寄与していないことがわかる.つまり,日最高気温と平均水蒸気圧以外に搬送人員数に影響する因子はない.最高気温が30.65℃以下では1日に約2名.30.65℃以上33.05℃未満では約9.5名.最高気温が33.05℃以上36.65℃未満では平均水蒸気圧が28.65mmHg未満で約19名,平均水蒸気圧が28.65mmHg以上で約29名.最高気温が36.65℃以上では約48名が搬送される.という意味になる.
オッカムの剃刀
オッカムの剃刀とは「ある事柄を説明するためには,必要以上に多くを仮定するべきでない」とする指針のことである.今回雲量や風速に関しては考察が不十分だが,説明変数として採用するのは見送る方針とした.
まとめ
交互作用項を考慮した最大モデルでは符号の正負,推定値の大きさに疑問があり,変数を減少させる必要があると考えられるが,その実践は難しい.一方,最小モデルではすべての変数が有意となったが予測性能が不足している.
樹木モデルによると搬送人員数に影響するのは日最高気温と平均水蒸気圧のみである.
