先の投稿では医科と歯科のファイルの分類が誤っていた.今回,正しく分類し直したので再度投稿する.
全国の医療機関コードを取得する
医療機関コードは10桁の数値からなる.最初の2桁が都道府県コード,次の1桁が区分点数コード,後半7桁が医療機関番号である.医療機関番号は都道府県内では一意であるが,都道府県をまたぐと一意ではなくなる.今回はその医療機関番号から医療機関コードを取得する方法を投稿する.
SQL Serverでサブクエリとウィンドウ関数とのパフォーマンスを比較する
SQL Serverでサブクエリとウィンドウ関数のパフォーマンスを比較した.用いたデータベースはHeatStrokeDBで,熱中症の搬送人員と最高気温との相関関係を可視化し閾値をχ二乗検定するで作成したものである.
比較するツールはSET STATISTCS PROFILE ONコマンドである.クエリストアは筆者の環境では機能しなかった.
“SQL Serverでサブクエリとウィンドウ関数とのパフォーマンスを比較する” の続きを読む
SQL Serverで空間インデックスを設定し空間演算を高速化する
データベースのテーブルに適切なインデックスを設定するのはクエリを高速化するうえで重要な施策である.今回,空間演算にコストがかかっていたクエリが空間インデックスの設定により高速化したので報告する.
二乗平均平方根誤差で回帰モデルの当てはまりを検討する
二乗平均平方根誤差とは英語では Root Mean Squared Error (RMSE) と書く.真値と予測値との乖離(誤差)を二乗し,その平均値をとり,その平方根を求めた値のことである.非負の値を取り,0に近いほど優れたモデルであることを示唆する.
今回使用するのはe-Statからの社会疫学的指標を加えて熱中症搬送人員数を分析するで使用したデータベースである.先の記事では回帰モデルを評価する指標が必要との認識であった.
社会疫学的指標を考慮した都道府県別の熱中症搬送人員数の予測と実際
都道府県別の熱中症搬送人員数の予測と実際をEXCELの組み合わせグラフで描くでは独立変数として日最高気温,日平均水蒸気圧,65歳以上人口,人口密度を投入し都道府県別の熱中症搬送人員数を予測した.以前の記事ではe-Statからの社会疫学的指標を加えて熱中症搬送人員数を分析した.社会疫学的指標としては日最高気温,日平均水蒸気圧,都道府県人口に加えて過去30日間の平均気温,エアコン保有台数,年間収入のジニ係数,光熱・水道費,実収入,第1次産業就業者比率,第2次産業就業者比率,都市公園数,都市緑化割合,自然公園割合,自然公園数,生活保護被保護人員である.
今回は社会疫学的指標を独立変数として加えた熱中症搬送人員数の予測と実際を示す.
e-Statからの社会疫学的指標を加えて熱中症搬送人員数を分析する
総務省の公開しているe-Statには社会疫学的指標が多く含まれる.今回熱中症搬送人員数に様々な指標を加えて解析してみた.
説明変数として日最高気温,日平均水蒸気圧,都道府県人口に加えて過去30日間の平均気温,エアコン保有台数,年間収入のジニ係数,光熱・水道費,実収入,第1次産業就業者比率,第2次産業就業者比率,都市公園数,都市緑化割合,自然公園割合,自然公園数,生活保護被保護人員を加えた.
すべての変数が有意であったが,VIFを見ると多重共線性を疑わせる変数もあり,良いモデルとは言えない結果となった.
日平均気温の過去30日間の移動平均をSQL Serverのウィンドウ関数を用いて計算する
熱中症の搬送人員数が月平均気温と負の相関があるとの情報を得た.普段涼しい地域ほど日最高気温の上昇に弱いという意味である.普段涼しいということを表現するには過去30日間の日平均気温の平均を取ればよいだろうと判断した.こうなるとSQL Serverのウィンドウ関数の出番である.
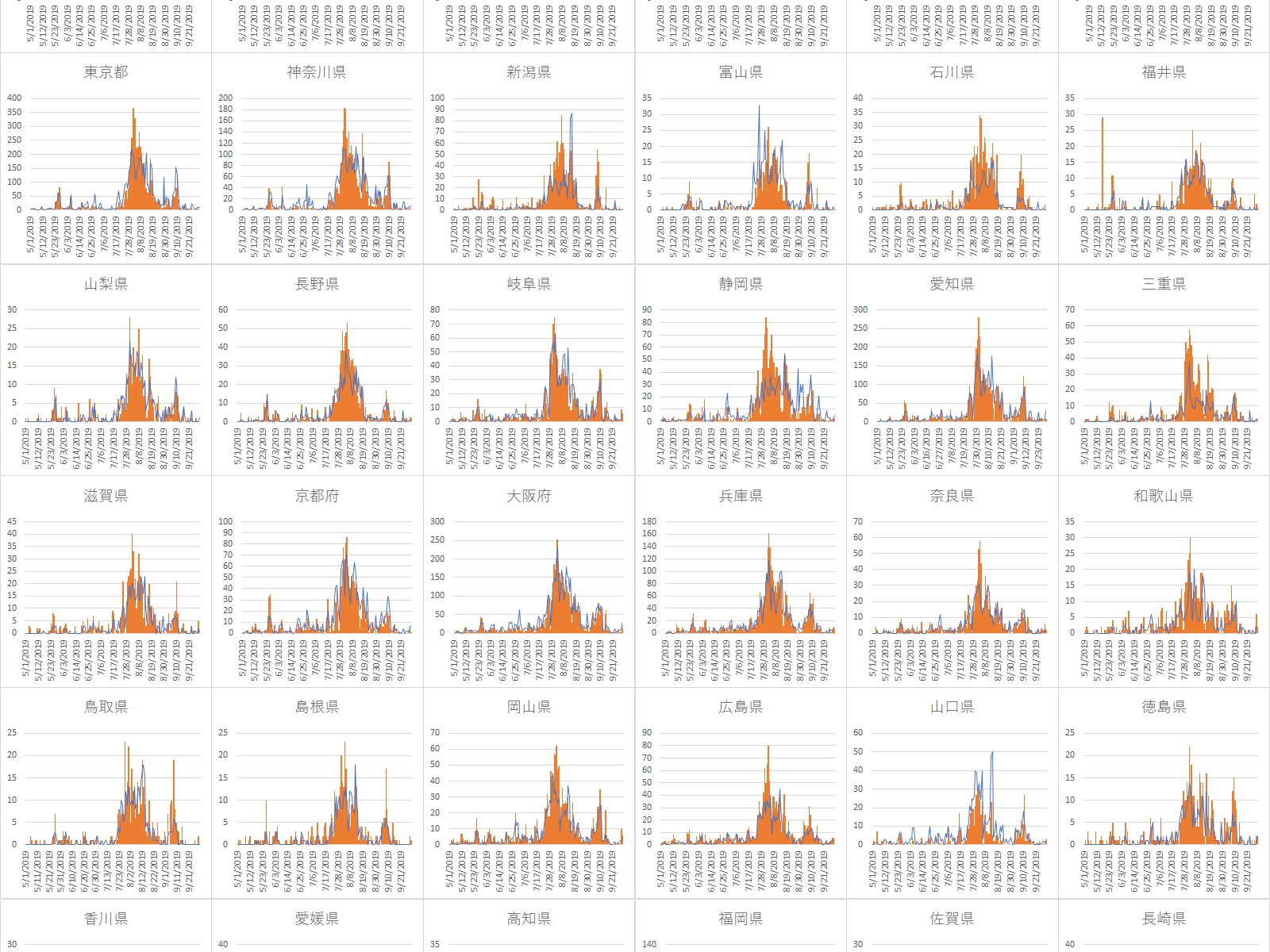
2019年の熱中症搬送人員数の予測と実際をEXCELの組み合わせグラフで描く
これまでの記事で日最高気温と平均水蒸気圧,各都道府県65歳以上人口および月から熱中症の搬送人員数を予測する回帰式の回帰係数を推定してきた.
今回はその回帰式を元に実際のデータと比較してみたい.対象は2019年の47都道府県とする.
熱中症搬送人員数のオフセット項を65歳以上人口に変更してみる
以前の記事では都道府県人口の対数をオフセット項として一般化線形回帰分析を行った.実際のところ,年代別の搬送人員としては65歳以上の高齢者が圧倒的に多い.そのため,東京など労働人口の多いところでは予測性能が悪化する可能性がある.今回はオフセット項の都道府県人口を3区分に分け,65歳以上人口の対数をオフセット項として採用してみたところ予測性能が改善したと思われたので記事とした.