統計解析に必ず出てくる正規分布.これを標準化した標準正規分布の数表は全部で 400 個に及ぶ数値が並んだ表である.教科書に記載されている数表は,端的に言って機械可読性に欠ける.テーブル形式にしたい.
NORM.S.DIST 関数を知る
この NORM.S.DIST 関数の罠は「下側確率」が仕様となっていることである.マイナス無限大から指定した Z 値まで確率密度関数を積分した面積が確率である,というのが下側確率の意味である.
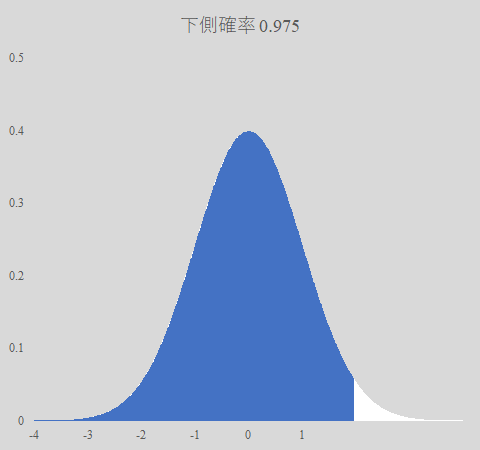
一方,標準正規分布の数表は「上側確率」である.指定した Z 値から無限大まで確率密度関数を積分した面積のことである.これを NORM.S.DIST 関数で直接求めるのは難しい.
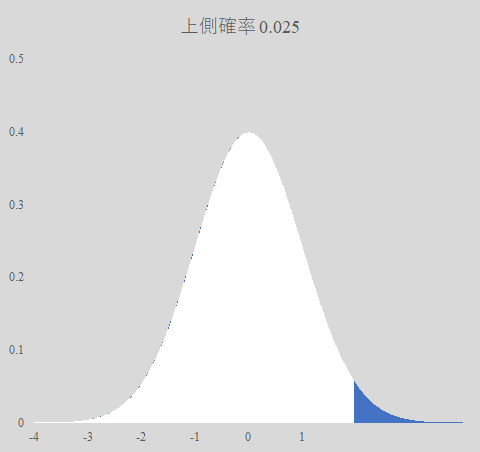
-3.99 から 0.00 まで 0.01 刻みに Z を 400 行作成する
面倒ではあるが,Z がマイナスいくつから 0 までの下側確率を求め,符号を反転させたほうが早そうだ.ここでは教科書の記載通り 400 個の数値を作成することにする.
ワークシートの A1 セルに Z とタイプし,B1 セルに P(Z) とタイプする.改行して A2 セルに下式のように入力する.
= (ROW()-401)/100
NORM.S.DIST 関数は下側確率を求める
B2 セルに下式のように入力する.第一引数に TRUE を指定すると「累積分布関数の値が計算される」と公式にはあるが,これはマイナス無限大から第一引数に指定した値 Z まで,確率密度関数を積分した面積,つまり下側確率のことである.
= NORM.S.DIST(A2, TRUE)
A1:B2 セルを選択してテーブルに変換する.A2:B2 セルを選択し,ドラッグして 400 行作成する.小数点以下の桁数は未設定であり,非常に小さい事がわかる.
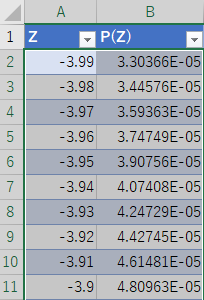
最終行の結果が 0.5 であることを確認してほしい.Z が 0 の時 P(Z) が 0.5 になっていなければ,それはこれまでの手順がおかしいことを示している.
A 列と B 列の間に 1 列挿入しマイナス1をかける
表示用の列を作成する.A 列と B 列の間に 1 列挿入する.新しい B2 セルに下式のようにタイプする.その結果,マイナス符号が消える.ここで下側確率が上側確率に変換される.
= A2*(-1)
全体をコピーして値を貼り付け
数式の参照関係を解消するために全体をコピーして「値の貼り付け」を行う.
Z で昇順ソート
最初の A 列を削除し,表示用に先刻挿入した列で昇順ソートを行う.下図ではすでに列名を Z と変更しており,A 列 (Z) の小数点以下の桁数を 2, B 列 (P(Z)) の小数点以下の桁数を 3 に変更している.
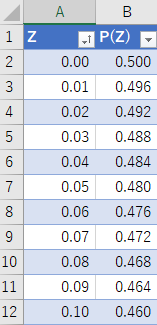
標準正規分布の上側確率の数表
結果を示す.覚えておくべき数値は Z = 1.28, 1.645, 1.96 である.それぞれP(Z) = 0.1, 0.05, 0.025 を返す.正確には下記の通りである.
- P( Z >= 1.96) = 0.025
- P(|Z|>= 1.96) = 0.05
- P( Z >= 1.645) = 0.05
- P(|Z|>= 1.645) = 0.1
- P( Z >= 1.28) = 0.1
特に 1.645 と 1.96 は片側検定,両側検定のときに間違えやすい.|Z| >= 1.96 などと絶対値記号がつけば両側検定,Z >= 1.96 などと絶対値記号がつかなければ片側検定と暫定的に覚えておきたい.
u Q(u) 0.00 0.500 0.01 0.496 0.02 0.492 0.03 0.488 0.04 0.484 0.05 0.480 0.06 0.476 0.07 0.472 0.08 0.468 0.09 0.464 0.10 0.460 0.11 0.456 0.12 0.452 0.13 0.448 0.14 0.444 0.15 0.440 0.16 0.436 0.17 0.433 0.18 0.429 0.19 0.425 0.20 0.421 0.21 0.417 0.22 0.413 0.23 0.409 0.24 0.405 0.25 0.401 0.26 0.397 0.27 0.394 0.28 0.390 0.29 0.386 0.30 0.382 0.31 0.378 0.32 0.374 0.33 0.371 0.34 0.367 0.35 0.363 0.36 0.359 0.37 0.356 0.38 0.352 0.39 0.348 0.40 0.345 0.41 0.341 0.42 0.337 0.43 0.334 0.44 0.330 0.45 0.326 0.46 0.323 0.47 0.319 0.48 0.316 0.49 0.312 0.50 0.309 0.51 0.305 0.52 0.302 0.53 0.298 0.54 0.295 0.55 0.291 0.56 0.288 0.57 0.284 0.58 0.281 0.59 0.278 0.60 0.274 0.61 0.271 0.62 0.268 0.63 0.264 0.64 0.261 0.65 0.258 0.66 0.255 0.67 0.251 0.68 0.248 0.69 0.245 0.70 0.242 0.71 0.239 0.72 0.236 0.73 0.233 0.74 0.230 0.75 0.227 0.76 0.224 0.77 0.221 0.78 0.218 0.79 0.215 0.80 0.212 0.81 0.209 0.82 0.206 0.83 0.203 0.84 0.200 0.85 0.198 0.86 0.195 0.87 0.192 0.88 0.189 0.89 0.187 0.90 0.184 0.91 0.181 0.92 0.179 0.93 0.176 0.94 0.174 0.95 0.171 0.96 0.169 0.97 0.166 0.98 0.164 0.99 0.161 1.00 0.159 1.01 0.156 1.02 0.154 1.03 0.152 1.04 0.149 1.05 0.147 1.06 0.145 1.07 0.142 1.08 0.140 1.09 0.138 1.10 0.136 1.11 0.133 1.12 0.131 1.13 0.129 1.14 0.127 1.15 0.125 1.16 0.123 1.17 0.121 1.18 0.119 1.19 0.117 1.20 0.115 1.21 0.113 1.22 0.111 1.23 0.109 1.24 0.107 1.25 0.106 1.26 0.104 1.27 0.102 1.28 0.100 1.29 0.099 1.30 0.097 1.31 0.095 1.32 0.093 1.33 0.092 1.34 0.090 1.35 0.089 1.36 0.087 1.37 0.085 1.38 0.084 1.39 0.082 1.40 0.081 1.41 0.079 1.42 0.078 1.43 0.076 1.44 0.075 1.45 0.074 1.46 0.072 1.47 0.071 1.48 0.069 1.49 0.068 1.50 0.067 1.51 0.066 1.52 0.064 1.53 0.063 1.54 0.062 1.55 0.061 1.56 0.059 1.57 0.058 1.58 0.057 1.59 0.056 1.60 0.055 1.61 0.054 1.62 0.053 1.63 0.052 1.64 0.051 1.65 0.049 1.66 0.048 1.67 0.047 1.68 0.046 1.69 0.046 1.70 0.045 1.71 0.044 1.72 0.043 1.73 0.042 1.74 0.041 1.75 0.040 1.76 0.039 1.77 0.038 1.78 0.038 1.79 0.037 1.80 0.036 1.81 0.035 1.82 0.034 1.83 0.034 1.84 0.033 1.85 0.032 1.86 0.031 1.87 0.031 1.88 0.030 1.89 0.029 1.90 0.029 1.91 0.028 1.92 0.027 1.93 0.027 1.94 0.026 1.95 0.026 1.96 0.025 1.97 0.024 1.98 0.024 1.99 0.023 2.00 0.023 2.01 0.022 2.02 0.022 2.03 0.021 2.04 0.021 2.05 0.020 2.06 0.020 2.07 0.019 2.08 0.019 2.09 0.018 2.10 0.018 2.11 0.017 2.12 0.017 2.13 0.017 2.14 0.016 2.15 0.016 2.16 0.015 2.17 0.015 2.18 0.015 2.19 0.014 2.20 0.014 2.21 0.014 2.22 0.013 2.23 0.013 2.24 0.013 2.25 0.012 2.26 0.012 2.27 0.012 2.28 0.011 2.29 0.011 2.30 0.011 2.31 0.010 2.32 0.010 2.33 0.010 2.34 0.010 2.35 0.009 2.36 0.009 2.37 0.009 2.38 0.009 2.39 0.008 2.40 0.008 2.41 0.008 2.42 0.008 2.43 0.008 2.44 0.007 2.45 0.007 2.46 0.007 2.47 0.007 2.48 0.007 2.49 0.006 2.50 0.006 2.51 0.006 2.52 0.006 2.53 0.006 2.54 0.006 2.55 0.005 2.56 0.005 2.57 0.005 2.58 0.005 2.59 0.005 2.60 0.005 2.61 0.005 2.62 0.004 2.63 0.004 2.64 0.004 2.65 0.004 2.66 0.004 2.67 0.004 2.68 0.004 2.69 0.004 2.70 0.003 2.71 0.003 2.72 0.003 2.73 0.003 2.74 0.003 2.75 0.003 2.76 0.003 2.77 0.003 2.78 0.003 2.79 0.003 2.80 0.003 2.81 0.002 2.82 0.002 2.83 0.002 2.84 0.002 2.85 0.002 2.86 0.002 2.87 0.002 2.88 0.002 2.89 0.002 2.90 0.002 2.91 0.002 2.92 0.002 2.93 0.002 2.94 0.002 2.95 0.002 2.96 0.002 2.97 0.001 2.98 0.001 2.99 0.001 3.00 0.001 3.01 0.001 3.02 0.001 3.03 0.001 3.04 0.001 3.05 0.001 3.06 0.001 3.07 0.001 3.08 0.001 3.09 0.001 3.10 0.001 3.11 0.001 3.12 0.001 3.13 0.001 3.14 0.001 3.15 0.001 3.16 0.001 3.17 0.001 3.18 0.001 3.19 0.001 3.20 0.001 3.21 0.001 3.22 0.001 3.23 0.001 3.24 0.001 3.25 0.001 3.26 0.001 3.27 0.001 3.28 0.001 3.29 0.001 3.30 0.000 3.31 0.000 3.32 0.000 3.33 0.000 3.34 0.000 3.35 0.000 3.36 0.000 3.37 0.000 3.38 0.000 3.39 0.000 3.40 0.000 3.41 0.000 3.42 0.000 3.43 0.000 3.44 0.000 3.45 0.000 3.46 0.000 3.47 0.000 3.48 0.000 3.49 0.000 3.50 0.000 3.51 0.000 3.52 0.000 3.53 0.000 3.54 0.000 3.55 0.000 3.56 0.000 3.57 0.000 3.58 0.000 3.59 0.000 3.60 0.000 3.61 0.000 3.62 0.000 3.63 0.000 3.64 0.000 3.65 0.000 3.66 0.000 3.67 0.000 3.68 0.000 3.69 0.000 3.70 0.000 3.71 0.000 3.72 0.000 3.73 0.000 3.74 0.000 3.75 0.000 3.76 0.000 3.77 0.000 3.78 0.000 3.79 0.000 3.80 0.000 3.81 0.000 3.82 0.000 3.83 0.000 3.84 0.000 3.85 0.000 3.86 0.000 3.87 0.000 3.88 0.000 3.89 0.000 3.90 0.000 3.91 0.000 3.92 0.000 3.93 0.000 3.94 0.000 3.95 0.000 3.96 0.000 3.97 0.000 3.98 0.000 3.99 0.000
まとめ
統計検定の基本である標準正規分布の上側確率の数表を計算で求め,表示した.
